Impact Force & Fall Factor Calculations (Pictures)
|
|
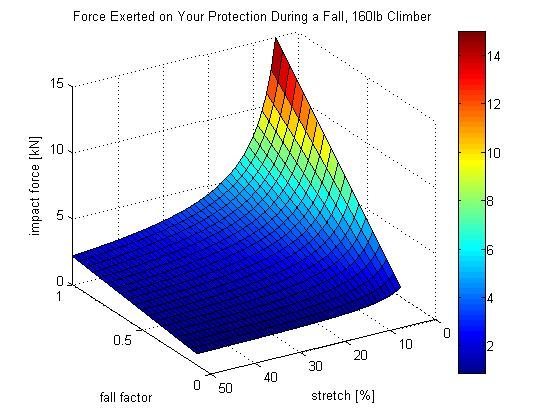
Three pages of hand-written calculations used to derive the formula for impact force (force felt by the rope and the protection placed in the wall during a climbing fall). I thought this would be useful since there's so much misleading information out there related to falls. The function simplifies so that impact force only depends on: The final plot shows impact force for different fall factor / rope stretch combinations (a.k.a. why a static rope cuts you in half) DISCLAIMER: Do not trust your life to any advice you hear from somebody on the internet - your safety is your own responsibility. |
|
|
Nice work - a few observations: |
|
|
Cody, as Chris points out, you are assuming a constant force applied by the rope, which is rather unrealistic. Your argument can be summarized as follows: The potential energy lost by the climber equals the work done by the rope. Under the assumption that the force is constant, (delta d1 + delta d2)mg = F(delta d2), from which your solution can be derived in a couple of easy steps. |
|
|
If you wanted a high-end estimate of the maximum force, I would take the average you calculated and double it. Your force estimate is a constant average force for a period of time/distance, if you were to plot this, it would be a rectangle, the area of which represents the energy absorbed, which should be correct. If we assume it follows a triangular profile, starting from 0 force, building to a peak, and tapering back down to 0 (really body weight, but we'll neglect that), then you can figure out the peak of that triangle by plugging in the same energy absorbed (area) into it... and it turns out that the peak force is double the average in this estimate. It's probably lower in reality as the curve will be more fluid, but it gives you a quick dirty upper bound. |
|
|
Also want to point out that the dynamic elongation variable you use is measured during a factor 1.7 fall with an 80kg mass, and the elongation is going to vary with the force applied. You could estimate this by interpolating the static and dynamic elongations. The static elongation is an 80kg mass factor 0 fall. |
|
|
Lets not forget that Brenta has a bad ass 'Climbing for Geeks' paper on the subject. Which he needs to complete and publish!!! |
|
|
Thanks for all the comments! I agree that it is a very simple model - I saw multiple posts on the forum in the last week to the effect of "nuh uh, climbing gear is rated for 200lb person...if you weigh more than that you should double up your slings" and that worried me quite a bit. I was mainly aiming to show the simple relationship between climber weight, fall factor, and rope elongation using only freshman-level physics equations to make the work accessible. |
|
|
brenta wrote:If you want a more sophisticated treatment, search the net for Tom Moyer's slides, or Dave Custer's. There's also a nice PDF by rgold that has been available for a while. You can download R. Gold's pdf here. An extension of that model that takes friction over the top anchor into account is available here. I also have an online impact force calculator, which uses both models. |
|
|
One thing you probably could do is take out 5% and under as not applicable with FF. I wonder if a lot of that elongation to FF could be cleaned out as to what is available for dynamics in the market. |
|
|
Chris Drover wrote:Nice work - a few observations: - Your calculation assumes that the impact force is constant while the rope is stretching. I would argue that this is not the case. Your calculation provides the average force during the deceleration, not the maximum, which is what UIAA defines "impact force" to be. - One way people have attempted to get around this is by treating the rope as a spring using Hooke's Law. Again, I would argue that this is not the case since this would rebound the climber back up to the hold he/she fell from (wouldn't that be awesome?!?). You could treat it as an overdamped oscillator, but without an experimental plot of force versus time during a fall (to determine the coefficients of the damping component), its all just speculation. Chris I found out on an overhanging top rope fall that the under-damped spring model works pretty well, too. Aside from swinging into space, there was noticeable oscillation along the length of the rope. Sadly, I was a little too young at the time to appreciate the implications for physical modeling of climber falls. :) |
|
|
I found the only problem to be that most people that don't already understand how much actual force is typically applied to an anchor/climber in a fall will never be able to understand the math or graphs! |

 Continue with onX Maps
Continue with onX Maps Sign in with Facebook
Sign in with Facebook